電気通信大学 2025年前期 数学解答まとめ

$\displaystyle -\frac{\pi}{2} \lt x \lt \frac{\pi}{2}$で定義された2つの関数 $$f(x) = \tan x + \frac{\sqrt{3}}{2} \cos x,\qquad g(x) = \frac{\sqrt{3}}{2} \cos x + \frac{2}{\sqrt{3}} \sin x$$ について，以下の問いに答えよ。

(配点 50)

(i) 不等式$\; f(x) \leqq g(x) \;$をみたす$\; x \;$の範囲を求めよ。

(ii) 曲線$\; y = f(x)\; $と$\; x \;$軸の共有点の$x$座標を$\; \alpha \;$，曲線$\; y = g(x) \;$と$\; x \;$軸の共有点の$\; x \;$座標を$\; \beta \;$とするとき，$\; \sin \alpha, \sin \beta \;$の値を求めよ。

(iii) 関数$\; g(x) \;$が$\; x = \gamma \;$で極値をとるとする。$\; \sin \gamma \;$の値を求めよ。

(iv) 次の不定積分を求めよ。ただし，積分定数は省略してもよい。

$$ I = \int \tan^2 x dx$$

(v) 不等式$\displaystyle \; 0\leqq x \lt \frac{\pi}{2}\;$の表す領域において曲線$\; y = f(x)\;$と$\; y = g(x) \;$で囲まれた部分を$\;D\;$とするとき，$\; D\; $を$\; x\;$軸のまわりに1回転させてできる立体の体積$\;V\;$を求めよ。

$\alpha \gt 0$とする。関数

$$f(x) = 2(x - 1)e^x - ax^2 + 5a$$について，以下の問いに答えよ。ただし，$\;e\;$は自然対数の底とする。 　　　　　(配点 50)

(i) 関数$\;f(x)\;$の導関数を$\;f'(x)\;$とする。方程式$\;f'(x) = 0 \;$を解け。

(ii) 関数$\; f(x)\;$が極小値0をもつような$\; \alpha \;$の値をすべて求めよ。

(iii) 次の不定積分を求めよ。ただし，積分定数は省略してもよい。

$$I = \int(x - 1) e^x dx$$

(iv) $\; a = 2\;$とし，曲線$\; y = f(x)\;$の上の点$\;(0, f(0))\;$における接線を$\; \ell\; $とする。曲線$\; y = f(x)\;$と接線$\; \ell \;$で囲まれた領域の面積$\; S\;$を求めよ。

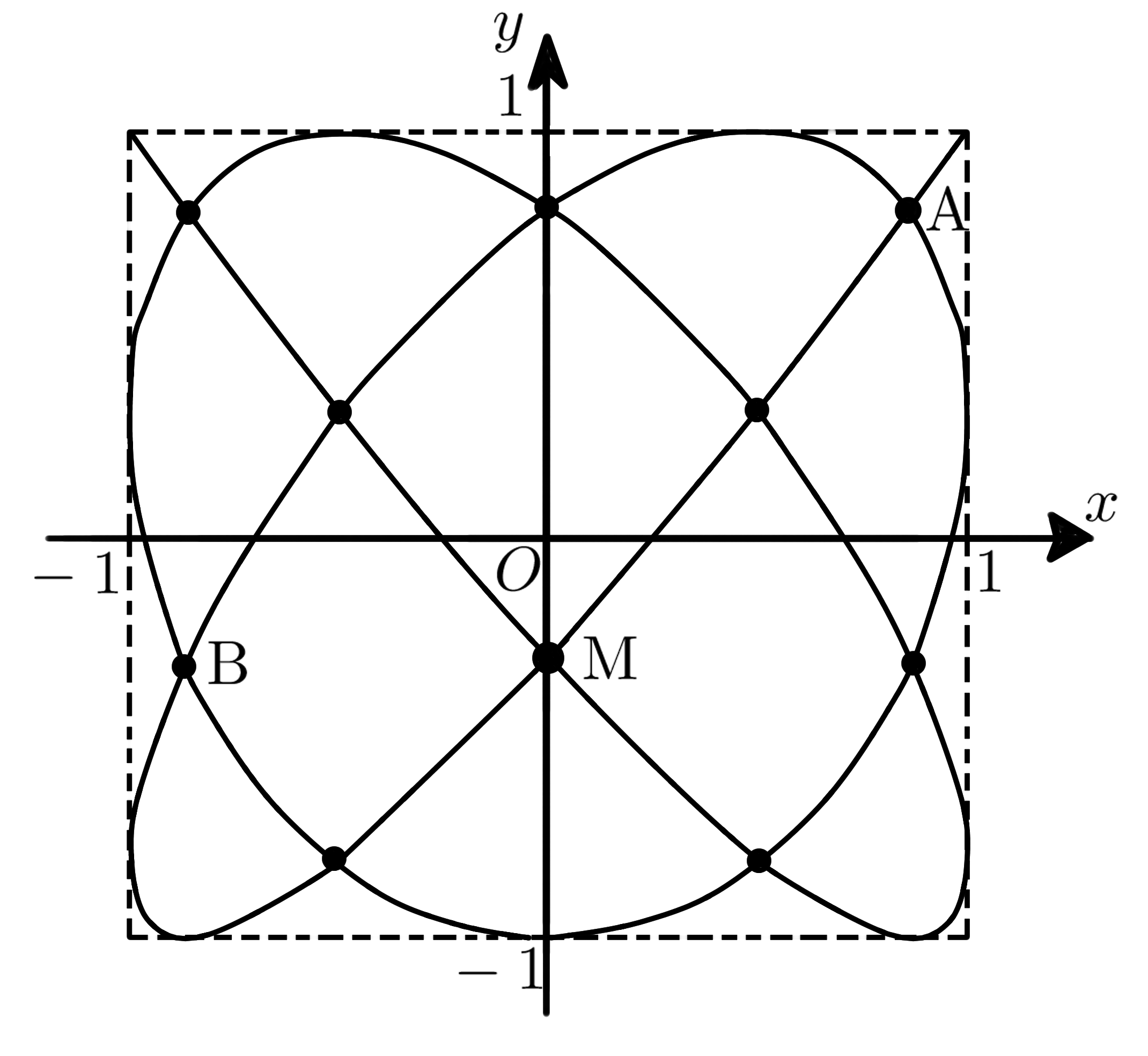
時刻$\;t\;$における座標が$$x = \cos 5t,\; y = \cos 6t \qquad (0 \leqq t \leqq \pi)$$で表される座標平面上の点$\; \mathrm{P}\;$の運動を考える。点$\; \mathrm{P} \;$がえがく曲線を$\;C\;$とする。曲線$\;C\;$の概形は下図のようになり，$\;t\;$が$\;0 \leqq t \leqq \pi\;$の範囲で動くとき点$\; \mathrm{P}\;$が2回通過する点は10個ある。そのうち3点$\; \mathrm{A, B, M}\;$を下図のようにとる。$\;\displaystyle \cos \frac{\pi}{5} = \frac{\sqrt{5} + 1}{4}\;$を用いて，以下の問いに答えよ。

(配点 50)

(i) 点$\; \mathrm{M}\;$は$\;y\;$軸上の$\;y \lt 0\;$の部分にある。点$\; \mathrm{M}\;$の$\;y\;$座標を，有理数$\; a, b\;$を用いて$\; a + b\sqrt{5}\;$の形で表せ。

(ii) $\; 0 \leqq t \leqq \pi\;$の範囲で次の方程式を解け。$$\cos 6t = \cos \frac{\pi}{5}$$

(iii) $\; \alpha_1 = \displaystyle{\frac{\pi}{30}}\;$とする。$\; t = \alpha_1\;$のとき，$\; (\cos 5\alpha_1, \; \cos 6\alpha_1)\;$は点$\; \mathrm{A}\;$である。$\; \alpha_1 \lt \alpha_2 \lt \pi\;$をみたすある値$\; \alpha_2\;$について，$\; t = \alpha_2\;$のときも$\; (\cos 5\alpha_2,\; \cos 6\alpha_2)\;$が点$\; \mathrm{A}\;$となる。この値$\; \alpha_2\;$を求めよ。

(iv) 点$\; \mathrm{M}\;$と第3象限の点$\; \mathrm{B}\;$は$\; y\;$座標が等しい。点$\; \mathrm{B}\;$の$\; x\;$座標を求めよ。また，直線$\; \mathrm{AB}\;$の方程式を，実数$\; m, n\;$を用いて$\; y= mx + n\;$の形で表せ。

次の条件によって定められる数列$\; \{a_n\}, \{b_n\}, \{c_n\}\;$を考える。

$$a_1 = 1,\qquad a_{n + 1} = b_n + c_n \qquad (n = 1, 2, 3, \cdots \cdots)$$ $$b_1 = 2,\qquad b_{n + 1} = c_n + a_n \qquad (n = 1, 2, 3, \cdots \cdots)$$ $$c_1 = 3,\qquad c_{n + 1} = a_n + b_n \qquad (n = 1, 2, 3, \cdots \cdots)$$

このとき，以下の問いに答えよ。

(配点 50)

(i) $\; a_2, b_2, c_2\;$を求めよ。

(ii) $\; a_n - b_n,\; c_n - b_n\;$をそれぞれ$\; n\;$の式で表せ。

(iii) 数列$\; \{b_n\}\;$の一般項を求めよ。

(iv) 数列$\; \{a_n\}\;$の一般項と数列$\; \{c_n\}\;$の一般項を求めよ。

(v) 無限級数$\; \displaystyle{\sum_{n = 1}^\infty \frac{a_n}{c_n}}\;$の収束，発散について調べ，収束するときにはその和を求めよ。